Capteur de masse NEMS

L’analyse des bifurcations permet de déterminer les changements de régime dynamique d’un système non-linéaire et d’anticiper les phénomènes indésirables tels que des sauts d’amplitude importants ou des instabilités. Des algorithmes originaux ont été développés (thèses L. Xie, C. Grenat) non seulement pour détecter et caractériser ces bifurcations, mais aussi pour suivre leur position lorsque les paramètres du système varient. Cette connaissance s’avère très utile car elle permet de contrôler l’apparition des bifurcations et donc d’optimiser le système lors de sa phase de conception.

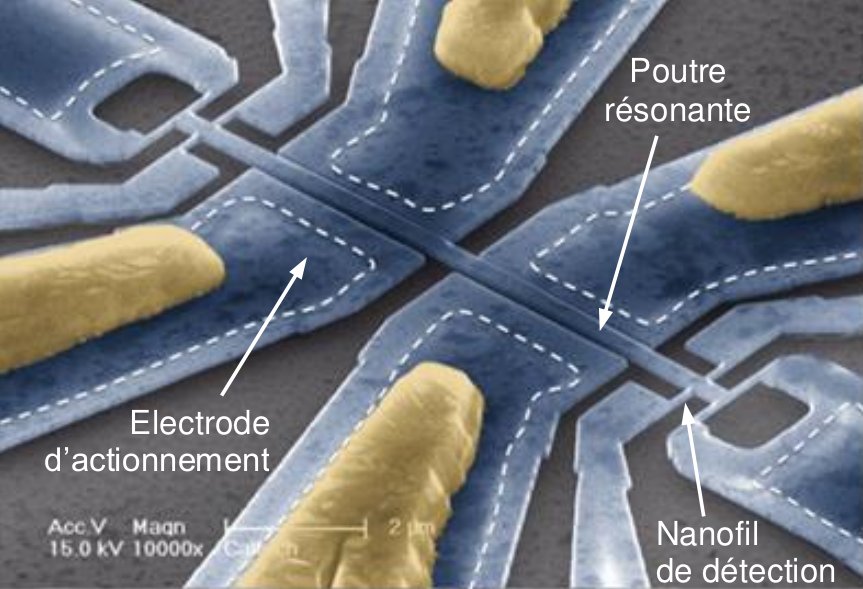
Plutôt que de subir les non-linéarités, une autre voie de recherche consiste à les exploiter. Les travaux initiés dans cette voie et concernant les capteurs résonants N/MEMS (nano/micro electromechanical systems) ont été poursuivis et étendus à des réseaux de plusieurs capteurs. Ils ont permis d’améliorer très nettement les méthodes de détection classiques et de proposer de nouveaux concepts de détection de masses infinitésimales (post-doc Nguyen, thèse C. Grenat) basés sur l’utilisation de phénomènes non-linéaires tels que les sauts d’amplitude, les boucles d’hystéresis ou encore les interactions modales. Ces nouveaux concepts ont conduit à un brevet et à une preuve de concept expérimentale en collaboration avec le CEA Leti (Grenoble).