Non-linear vibrations : Parametric analysis of bifurcations - Exploiting non-linearities
Bifurcation analysis can be used to determine changes in the dynamic regime of a non-linear system and to anticipate undesirable phenomena such as large jumps in amplitude or instabilities. Original algorithms have been developed (theses L. Xie, C. Grenat) not only to detect and characterise these bifurcations, but also to track their position when the system parameters vary. This knowledge is very useful, as it allows us to control the appearance of bifurcations and therefore to optimise the system during the design phase.
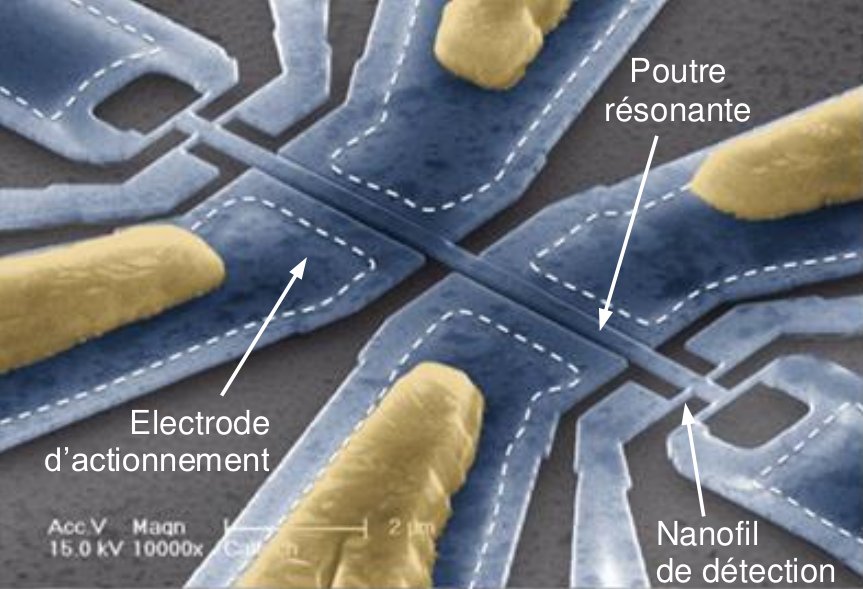
Rather than being subjected to non-linearities, another avenue of research involves exploiting them. Work in this area, which began with N/MEMS (nano/micro electromechanical systems) resonant sensors, has been continued and extended to networks of several sensors. This work has led to significant improvements in conventional detection methods and to the development of new concepts for the detection of infinitesimal masses (post-doc Nguyen, thesis C. Grenat) based on the use of non-linear phenomena such as amplitude jumps, hysteresis loops and modal interactions. These new concepts have led to a patent and an experimental proof of concept in collaboration with CEA Leti (Grenoble).
Rather than being subjected to non-linearities, another avenue of research involves exploiting them. Work in this area, which began with N/MEMS (nano/micro electromechanical systems) resonant sensors, has been continued and extended to networks of several sensors. This work has led to significant improvements in conventional detection methods and to the development of new concepts for the detection of infinitesimal masses (post-doc Nguyen, thesis C. Grenat) based on the use of non-linear phenomena such as amplitude jumps, hysteresis loops and modal interactions. These new concepts have led to a patent and an experimental proof of concept in collaboration with CEA Leti (Grenoble).
Contact : BAGUET Sébastien