Relative Displacements and Strain

In this topic, you will find general information about Transformation gradient tensor and strain tensors.

Transformation Gradient Tensor

The relation linking the initial relative position and the instantaneous relative position is :

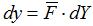
with :

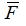• : Transformation gradient tensor,

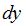• : Instantaneous relative position,

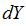• : Initial relative position.

The transformation gradient tensor can be written in a multiplicative decomposition as deformation and rotation :

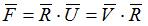
with :

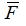• : Transformation gradient tensor,

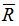• : Rotation tensor,

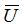• : Right stretch,

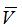• : Left stretch.

The multiplicative decomposition can be resumed in the following example :

Multiplicative decomposition of the transformation gradient tensor

Cauchy Green Strain Tensor

Cauchy Green strain is given by the following relation :

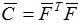the eigenvalues are noted C1 and C2.

Green Lagrange Strain Tensor

Green Lagrange strain is given by the following relation :

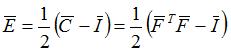
with :

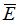• : Green Lagrange strain tensor

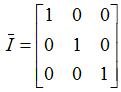• : Identity matrix.

Hencky Strain Tensor

Hencky strain tensor is given by the following relation :

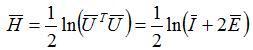
with :

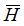• : Hencky strain tensor,

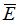• : Green Lagrange strain tensor.

Shear angle

,

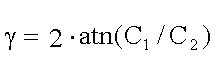C1 and C2 are the eigenvalues of Cauchy Green tensor.